Estadística
La Estadística trata del recuento, ordenación y clasificación de los datos obtenidos por las observaciones, para poder hacer comparaciones y sacar conclusiones.
Un estudio estadístico consta de las siguientes fases:
· Recogida de datos.
· Organización y representación de datos.
· Análisis de datos.
· Obtención de conclusiones.
Conceptos de Estadística
Población: Una población es el conjunto de todos los elementos a los que se somete a un estudio estadístico.
Individuo: Un individuo o unidad estadística es cada uno de los elementos que componen la población.
Muestra: Una muestra es un conjunto representativo de la población de referencia, el número de individuos de una muestra es menor que el de la población.
Muestreo: El muestreo es la reunión de datos que se desea estudiar, obtenidos de una proporción reducida y representativa de la población.
Valor: Un valor es cada uno de los distintos resultados que se pueden obtener en un estudio estadístico. Si lanzamos una moneda al aire 5 veces obtenemos dos valores: cara y cruz.
Dato: Un dato es cada uno de los valores que se ha obtenido al realizar un estudio estadístico. Si lanzamos una moneda al aire 5 veces obtenemos 5 datos: cara, cara, cruz, cara, cruz.
Variable estadística
Definición de variable: Una variable estadística es cada una de las características o cualidades que poseen los individuos de una población.
TIPOS DE VARIABLE ESTADÍSTICAS:
Variable cualitativa: Las variables cualitativas se refieren a características o cualidades que no pueden ser medidas con números. Podemos distinguir dos tipos:
Variable cualitativa nominal: Una variable cualitativa nominal presenta modalidades no numéricas que no admiten un criterio de orden.
Por ejemplo: El estado civil, con las siguientes modalidades: soltero, casado, separado, divorciado y viudo.
Variable cualitativa ordinal o: Una variable cualitativa ordinal presenta modalidades no númericas, variable cuasicuantitativa en las que existe un orden.
Por ejemplo: La nota en un examen: suspenso, aprobado, notable, sobresaliente.
Puesto conseguido en una prueba deportiva: 1º, 2º, 3º, ...
Medallas de una prueba deportiva: oro, plata, bronce.
Variable cuantitativa: Una variable cuantitativa es la que se expresa mediante un número, por tanto se pueden realizar operaciones aritméticas con ella. Podemos distinguir dos tipos:
Variable discreta: Una variable discreta es aquella que toma valores aislados, es decir no admite valores intermedios entre dos valores específicos. Por ejemplo:
El número de hermanos de 5 amigos: 2, 1, 0, 1, 3.
Tablas de estadística
Distribución de frecuencias: La distribución de frecuencias o tabla de frecuencias es una ordenación en forma de tabla de los datos estadísticos, asignando a cada dato su frecuencia correspondiente.
TIPOS DE FRECUENCIAS:
Frecuencia absoluta: La frecuencia absoluta es el número de veces que aparece un determinado valor en un estudio estadístico. Se representa por fi.
La suma de las frecuencias absolutas es igual al número total de datos, que se representa por N.
Para indicar resumidamente estas sumas se utiliza la letra griega Σ (sigma mayúscula) que se lee suma o sumatoria.
Frecuencia relativa: La frecuencia relativa es el cociente entre la frecuencia absoluta de un determinado valor y el número total de datos.
Se puede expresar en tantos por ciento y se representa por ni.
La suma de las frecuencias relativas es igual a 1.
Frecuencia acumulada: La frecuencia acumulada es la suma de las frecuencias absolutas de todos los valores inferiores o iguales al valor considerado.
Se representa por Fi.
Frecuencia relativa acumulada: La frecuencia relativa acumulada es el cociente entre la frecuencia acumulada de un determinado valor y el número total de datos. Se puede expresar en tantos por ciento.
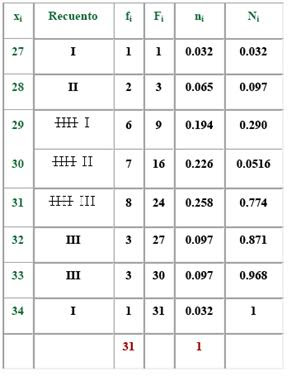
Durante el mes de julio, en una ciudad se han registrado las siguientes temperaturas máximas:
32, 31, 28, 29, 33, 32, 31, 30, 31, 31, 27, 28, 29, 30, 32, 31, 31, 30, 30, 29, 29, 30, 30, 31, 30, 31, 34, 33, 33, 29, 29.
En la primera columna de la tabla colocamos la variable ordenada de menor a mayor, en la segunda hacemos el recuento y en la tercera anotamos la frecuencia absoluta.
Este tipo de tablas de frecuencias se utiliza con variables discretas.
Diagrama de barras: Un diagrama de barras se utiliza para de presentar datos cualitativos o datos cuantitativos de tipo discreto.
Se representan sobre unos ejes de coordenadas, en el eje de abscisas se colocan los valores de la variable, y sobre el eje de ordenadas las frecuencias absolutas o relativas o acumuladas.
Los datos se representan mediante barras de una altura proporcional a la frecuencia.
Ejemplo
Un estudio hecho al conjunto de los 20 alumnos de una clase para determinar su grupo sanguíneo ha dado el siguiente resultado:
Polígonos de frecuencia: Un polígono de frecuencias se forma uniendo los extremos de las barras mediante segmentos.
También se puede realizar trazando los puntos que representan las frecuencias y uniéndolos mediante segmentos.
Ejemplo
Las temperaturas en un día de otoño de una ciudad han sufrido las siguientes variaciones:
Se utilizan para variables contínuas o para variables discretas, con un gran número de datos, y que se han agrupado en clases.
En el eje abscisas se construyen unos rectángulos que tiene por base la amplitud del intervalo, y por altura, la frecuencia absoluta de cada intervalo.
La superficie de cada barra es proporcional a la frecuencia de los valores representados.
Polígono de frecuencia: Para construir el polígono de frecuencia se toma la marca de clase que coincide con el punto medio de cada rectángulo.
Ejemplo
El peso de 65 personas adultas viene dado por la siguiente tabla:
Histograma y polígono de frecuencias acumuladas
Si se representan las frecuencias acumuladas de una tabla de datos agrupados se obtiene el histograma de frecuencias acumuladas o su correspondiente polígono.
Medidas de centralización
Nos indican en torno a qué valor (centro) se distribuyen los datos.
La medidas de centralización son:
Media aritmética: La media es el valor promedio de la distribución.
Mediana: La mediana es la puntación de la escala que separa la mitad superior de la distribución y la inferior, es decir divide la serie de datos en dos partes iguales.
Moda: La moda es el valor que más se repite en una distribución.
Medidas de dispersión
Las medidas de dispersión nos informan sobre cuánto se alejan del centro los valores de la distribución.
Las medidas de dispersión son:
Rango o recorrido: El rango es la diferencia entre el mayor y el menor de los datos de una distribución estadística.
Desviación media: La desviación media es la media aritmética de los valores absolutos de las desviaciones respecto a la media.
Varianza: La varianza es la media aritmética del cuadrado de las desviaciones respecto a la media.
Desviación típica: La desviación típica es la raíz cuadrada de la varianza.
Moda: La moda es el valor que tiene mayor frecuencia absoluta. Se representa por Mo.
Se puede hallar la moda para variables cualitativas y cuantitativas.
Hallar la moda de la distribución: 2, 3, 3, 4, 4, 4, 5, 5. Mo= 4
Si en un grupo hay dos o varias puntuaciones con la misma frecuencia y esa frecuencia es la máxima, la distribución es bimodal o multimodal, es decir, tiene varias modas.
1, 1, 1, 4, 4, 5, 5, 5, 7, 8, 9, 9, 9. Mo= 1, 5, 9
Cuando todas las puntuaciones de un grupo tienen la misma frecuencia, no hay moda.
2, 2, 3, 3, 6, 6, 9, 9
Si dos puntuaciones adyacentes tienen la frecuencia máxima, la moda es el promedio de las dos puntuaciones adyacentes.
0, 1, 3, 3, 5, 5, 7, 8. Mo = 4
Mediana: Es el valor que ocupa el lugar central de todos los datos cuando éstos están ordenados de menor a mayor. La mediana se representa por Me.
La mediana se puede hallar sólo para variables cuantitativas.
Cálculo de la mediana:
- Ordenamos los datos de menor a mayor.
- Si la serie tiene un número impar de medidas, la mediana es la puntuación central de la misma. 2, 3, 4, 4, 5, 5, 5, 6, 6. Me= 5
- Si la serie tiene un número par de puntuaciones la mediana es la media entre las dos puntuaciones centrales. 7, 8, 9, 10, 11, 12. Me= 9.5
Media aritmética
Definición de media aritmética: La media aritmética es el valor obtenido al sumar todos los datos y dividir el resultado entre el número total de datos. X es el símbolo de la media aritmética.
Ejemplo
Los pesos de seis amigos son: 84, 91, 72, 68, 87 y 78 kg. Hallar el peso medio.
6
Ejemplo de media aritmética
En un test realizado a un grupo de 42 personas se han obtenido las puntuaciones que muestra la tabla.
Calcula la puntuación media.
Observaciones sobre la media aritmética:
- La media se puede hallar sólo para variables cuantitativas.
- La media es independiente de las amplitudes de los intervalos.
- La media es muy sensible a las puntuaciones extremas. Si tenemos una distribución con los siguientes pesos: 65 kg, 69kg , 65 kg, 72 kg, 66 kg, 75 kg, 70 kg, 110 kg.
La media es igual a 74 kg, que es una medida de centralización poco representativa de la distribución.
- La media no se puede calcular si hay un intervalo con una amplitud indeterminada.
En este caso no es posible hallar la media porque no podemos calcular la marca de clase del último intervalo.
ACTIVIDADES
1. Clasifica en cualitativos y cuantitativos los siguientes caracteres estadísticos de un grupo de alumnos:
a) Grupo sanguíneo.
b) Profesión del padre.
c) Número de llamadas telefónicas que han realizado en una semana.
d) Paga semanal que reciben.
2. Clasifica en discretas y continuas las siguientes variables estadísticas:
a) Edad de la madre de los alumnos de una clase de 4º de ESO.
b) Talla de calzado que usan los alumnos de una clase de 4º de ESO.
c) Cotización diaria de las acciones de una empresa en el mercado de divisas.
3. En el estudio del número de hermanos que componen las familias de los alumnos de una clase con 32 estudiantes, se obtuvo la siguiente distribución de frecuencias:
xi (nº hermanos | 1 | 2 | 3 | 4 | 5 |
Fi (frecuencia) | 6 | 12 | 8 | 4 | 2 |
a) Construye la tabla de frecuencias absolutas y relativas.
b) Halla la media, la mediana y la moda de la distribución.
c) Halla el rango de la distribución4. Las edades de las personas que van en un autobús de línea en un momento determinado son: 52, 71, 17, 40, 62, 9, 67, 27, 5, 48, 8, 32, 51, 75, 9, 14, 40, 35, 56, 45.
a) Agrupa los datos en intervalos de amplitud 10.
b) Construye la tabla de frecuencias absolutas y relativas y absolutas y relativas acumuladas.
c) Halla la media, la mediana y el rango de la distribución.
d) Representa los datos en un diagrama de barras.5. El siguiente diagrama de barras muestra el número de horas que dedica diariamente a practicar deporte un grupo de 25 jóvenes.
a) Halla la media y la desviación típica de la distribución.
b) Calcula el porcentaje de datos que se encuentran en el intervalo ( X̄ - Sl X̄ + S)
6. El tiempo, en minutos, que un grupo de 20 alumnos tarda en llegar a su centro escolar por la mañana, viene reflejado en la siguiente tabla:
a) Construye la tabla de frecuencias absolutas y relativas.
b) Halla la media, la mediana y la moda de la distribución.
c) Halla la desviación media, la varianza y la desviación típica.