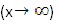LÍMITE DE UNA FUNCIÓN

Siempre cuando se  presenta un nuevo tema, la pregunta que surge entre nuestros alumnos es:   
                                                                                                                                               
¿Qué  aplicaciones  tiene  el  tema?  ¿Se aplica en hechos cotidianos?

Son las preguntas de nuestros alumnos, pregunta que según sea la respuesta, el tema se aprende mejor o no.   Para ello les voy a presentar una serie de situaciones donde vamos a aplicar el tema, pero recuerden que estos ejemplos se consiguen en libros,pero para nuestros alumnos, este medio puede ser más accesible y más rápido para encontrar las respuestas que siempre están buscando.

 1- El precio en euros de x litros de aceite viene dado por la función: 
 

a)         Determina el valor de la constante a para que la función f(x) sea continua.

b)         ¿A cuánto sale el litro si se compran 15, 20, 50 y 100 litros?

c)         Si se comprasen muchísimos litros de aceite, ¿a cuánto saldría aproximadamente el precio de cada litro?

 RESPUESTAS:

a)      El único punto que plantea problemas de continuidad es x = 20, que es el valor que marca la posible diferencia de precios. Para que sea continua, debe cumplirse que los límites laterales coincidan en dicho punto con P (20) = 60. Por la izquierda:

                                                                     Como debe cumplirse que:

       Si a = 4, la función será continua, siendo:

                                                                                                                                                                                                             b)   El costo de 15 litros es P (15) = 3.5                                P(15)=45. Cada litro sale a 3 €. 
             Para 20 litros, P (20) = 60. El precio sigue siendo de 3 € por litro.

   Para 50 litros, P (50) = raíz cuadrada de 12000 = 109,54; el litro sale 109,54/ 50 = 2,19 €.     

Para 100 litros, P(100) =  raíz cuadrada de 42000  =  204,94; el litro sale a 2,05 €.
                                                                                                     

c)      El costo unitario (costo por cada litro si se comparan x litros) vendrá dado por la función:

                                                                                Cuando x se hace muy grande, el costo unitario tiende a: 

  

            

El precio del litro de aceite se va acercando cada vez más a 2€.

      

    2-    Un alimento se introduce en un congelador. Si su temperatura ( en °C) viene dada  por  la      

fórmula                                                                                                                                                     

donde x indica las horas que lleva en el  congelador, se pide:

a)      ¿Qué temperatura tenía cuando se introdujo?

b)      ¿A qué temperatura estará al cabo de 2 horas?

c)      ¿A qué temperatura tiende con el paso del tiempo?

RESPUESTA:

a)              T (0) = 12/2 = 6°C.

    A las 2 hs, 

=>     T(2) =-26/8 = -3,25°C. 

  Cuando el tiempo se va alargando   la temperatura del alimento tiende a 

                                                                             

Se proponen las actividades siguientes:        

1-      Si estimamos que el número de pulsaciones por minuto que es capaz de teclear una persona que aprende mecanografía viene dado por la función

,

 donde x expresa el número de horas de gráfica (x ≥ 0) ,¿ a cuánto tiende el número de pulsaciones cuando x se hace muy grande?

Resp: 350

2- Cuando una persona se cambia de ciudad comienza un proceso paulatino de conocimiento  de su nuevo hábitat. Supongamos que el porcentaje de ciudad   (calles, plazas, edificios,….) que va conociendo viene dado por el valor de la función   

      ¿A qué tiende f(x) con el transcurso del tiempo?

Resp: 100

3-      El precio de la furgoneta fue de € 25000. Se estima, además, que el costo de uso y mantenimiento es de  0,20 € por km. Determina:

a)      La expresión analítica de la función que da el de costo  por km dependiendo de los km x recorridos.

b)      Si la furgoneta funcionase indefinidamente, ¿a cuánto tendería ese costo? Da una explicación gráfica de ese resultado.

     Resp:      a)                                               b)                                                   

      = f(x)                                              0,20                             

ACERTIJO

1) EL PRECIO DE LOS HUEVOS

"Pagué doce centavos por los huevos que compré al almacenero", explicó la cocinera, "pero le hice darme dos huevos extra porque eran muy pequeños. Eso hizo que el total sumara un centavo menos por docena que el primer precio que me dio."


¿Cuántos huevos compró la cocinera?


2) COSTOS CONTRACTUALES

Un contratista abocado a la construcción de una casa descubrió que debía pagar:

$ 1.100 al empapelador y al pintor,

$ 1.700 al pintor y al plomero,

$ 1.100 al plomero y al electricista,

$ 3.300 al electricista y al carpintero,

$ 5.300 al carpintero y al albañil,

$ 2.500 al albañil y al empapelador.


¿Cuánto cobra por sus servivios cada uno de ellos?


3- Una señora se olvida en casa el permiso de conducir. No se detiene en un paso nivel, desprecia una señal de dirección prohibida y viaja tres bloques en dirección contaría por una calle de sentido único. Todo esto es observado por un agente de tráfico, quien, sin embargo, no hace el menor intento de impedírselo. ¿Por qué?

4- Qué hora será, si queda del día la tercera parte de las horas que han pasado?

5- El perro de Juan está atado por el cuello a una cuerda de 3 m de longitud.

¿Cómo podrá alcanzar un sabroso hueso situado a 5m de él?

6- Un ladrillo pesa 2 kg más medio ladrillo. ¿Cuánto pesará un ladrillo y medio?

7- La suma de tres cifras iguales, que no son tres veintes, da como resultado 60.

¿Qué cifras son?

8- ¿Cuánta tierra hay en un agujero de 30x30x30 metros?

9- ¿Cuánto tiempo necesitamos para cocer un huevo duro?

10- ¿Cómo podemos poner 9 caramelos en 4 cajas de forma que cada una tenga un número impar de caramelos y distinto del de cada una de las tres?

11- Dos astronautas suben a la nave y parten hacia el espacio exterior. Llegan al cabo de unos días a su destino, y lo sorprendente es que, sin aterrizar, bajan tranquilamente de la nave, dan un paseo y vuelven a subir a la nave. ¿Cómo han podido hacer tal cosa?

12- Una botella de refresco cuesta 10 euros. El refresco cuesta 9 euros más que la botella. ¿Cuánto cuesta la botella?

13- ¿Qué necesitas para poder cerrar una puerta?

14- Julia llevo al joyero 6 trozos de cadena, cada uno de los cuales tenía 5 eslabones. Quería unir los 6 trozos de cadena para formar una gran cadena circular. Julia preguntó al joyero cuánto le costaría. Éste le contestó que cada eslabón que tuviera que abrir y volver a cerrar le costaría 3n euros. ¿Cuál es el precio mínimo que deberá pagar Julia al joyero para que elabore esa nueva joya?

15- Había 2 caballos orientados en direcciones opuestas: uno miraba directamente hacia el este, y el otro hacia el oeste. ¿Qué tuvieron que hacer para verse uno al otro sin necesidad de caminar, girar, o incluso mover la cabeza?

16- Ana y Gema hicieron a primeros de año una visita a Madrid. Llegaron a la ciudad con solo 30 euros cada uno. No pidieron dinero prestado ni les tocó la primitiva. El día 10 de enero de ese mismo año tenían más de cien mil euros entre las dos. ¿Cómo lo consiguieron?

17- En la cima de la montaña encontramos un sombrero, una bufanda y una zanahoria. Nadie ha tirado estos tres objetos al suelo, pero es totalmente lógico que se encuentren juntos en ese lugar. ¿Cuál es la explicación?

SOLUCIONES PROPUESTAS EXAMEN "Dic. 2010"

SOLUCIONES  de  las  PROPUESTAS   de  EXAMEN    2do BACH.      “Dic. 2010”

PROPUESTA   Nº 1:  

1-  a) Calculo las combinaciones de 10 en 7 = 120

      b) Calculo las combinaciones de 6 en 3 = 20.

2- a)

 

	Usan   lentes	No  usan  lentes	Total
Niños	280	320	600
Niñas	118	282	400
Total	398	602	1000

  b)  La probabilidad de que sea niña es =400/1000, es decir P = 0,4 c)  La probabilidad de que sea niña y que use lentes es =  118/400, es decir P = 0,295. 

                                                 

3- a) Ecuación  de  la recta  paralela a  r) 2x – y + 4 = 0  pasa por A(-2; 1).

     Para  ello  despejo    y = 2x + 4  

   La  paralela  sería   y = 2x + n  y  como pasa por A,

      entonces  sustituimos   1 = 2(-2) +n

       1 = -4 +n        

1 + 4 = n

    5 = n    , la ecuación es:    y = 2x + 5.

   b) La ecuación de la circunferencia.

El punto C es el centro de la circunferencia, por lo tanto  α = 4  y  β = -3.                                                                   D (2; 1);  punto  de  la  circunferencia. Entonces debemos calcular la distancia entre los puntos C  y D

para así obtener el radio. Realizados los cálculos correspondientes el r = √20 .                               x² + y² ax +by +c = 0 ;  ecuación  de la circunferencia, sabemos que:                a = -2α

b = -2β                      c = α² + β² – r².

Entonces  haciendo las operaciones: a = -8     b = 6  y  c = 5,

por  lo que la  ecuación  de la  circunferencia  es:  x² + y² – 8x + 6y + 5 = 0.

4-  a) La opción correcta es   ii) 10 ,  donde debes realizar: P(-2) = -4(-2)³ + 5(-2) – 12,

   al resolver las operaciones  se obtiene que P(-2) = 10, lo que justifica la respuesta.

 

      b)  Determina  c,  Q (2) = 3(2)³ – 2² + 2c – 3        Q(2) = 7          Q (2) = 24 – 4 + 2c – 3

     24 – 4 + 2c – 3 = 7                         17 + 2c = 7

    2c = 7 – 17                                  c =-10/2        ⇾  c = -5

 

PROPUESTA   Nº   2:

1- Ejercicio  correspondiente al gráfico de la función  f(x) de 3er grado.

Teniendo en cuenta los datos que se observan en el gráfico, podemos escribir:

f(x) = a(x –α) (x – β) (x – γ)

f(0) = 1  ⇒ f(x) = a(0 + 3)(0 + 1)(0 – γ)

a . 3 . 1 (-γ) = -1

-3 a γ = -1                a γ = 1/3                                                                                                                         f(2) = 5  ⇒ f(2) = a(2 +3)(2 +1)( 2- γ)

       15 a (2 – γ) = 5

       30 a – 15 a γ = 5     como  a γ = 1/3, sustituimos

       30 a – 15(1/3) = 5    realizo operaciones

       a = 10/30                  a = 1/3

                                                                                                                                      

    a γ = 1/3  entonces      1/3 γ = 1/3

γ = 1  raíz que se debía calcular.

La  forma  factorizada  de  la función  es:         f(x) = 1/3(x +3)(x +1)(x -1).

2-  a) Ecuación de la recta que pasa por los puntos A(3; 0) y B(-1; -2).

     (x – x₂) (y – y₁) = (x – x₁) (y – y₂)

       ( x -0)( y + 1) = ( x – 3) ( y + 2)

       xy + x = xy + 2x – 3y – 6   por   prop. Cancelativa 

       x – 2x + 3y + 6 = 0

       -x + 3y + 6 = 0   ecuación de la recta AB.

b)  Recta   “t” paralela  a  AB  que  pasa por  M (2; 1).

  -x + 3y + 6 = 0

   y = 1/3 x – 2    su  paralela es  y = 1/3 x + n  y pasa  por  M.

                                       1 = 1/3 (2) + n

                                                      1 = 2/3  + n       1 -2/3   = n   ⇒   1/3 = n

   y = 1/3 + 1/3    ecuación   paralela  a  la  recta  AB.

c) Ecuación de la circunferencia coincide con la  parte b) del ejercicio 3 de la propuesta Nº 1.